What is 6/12 + 1/6?

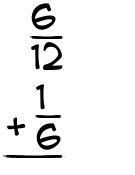
Here's how we add

Step 1

Our denominators (bottom numbers) don't match, so we can't add yet.

12 goes into 6 evenly, so we only need to multiply one term to get a common denominator.

Multiply 1 by 2, and get 2, then we multiply 6 by 2 and get 12.

This gives us a new problem that looks like so:

Step 2

Since our denominators match, we can add the numerators.

6 + 2 = 8

That gives us an answer of

Step 3

Can this fraction be reduced?

First, we attempt to divide it by 2...

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

Now, try the same number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

Now, try the same number again.

Nope. Try the next prime number, 3...

No good. 3 is larger than 2. So we're done reducing.

Congratulations! Here's your final answer to 6/12 + 1/6