What is 64/16 + 6/12?

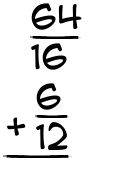
Here's how to add

Step 1

Of course, you can't add two fractions if the denominators (bottom numbers) don't match. To get a common denominator, multiply the denominators together. Then we fix the numerators by multiplying each one by their other term's denominator.

Now you multiply 64 by 12, and get 768, then we multiply 16 by 12 and get 192.

Do the same for the second term. We multiply 6 by 16, and get 96, then multiply 16 by 12 and get 192.

The problem now has new fractions to add:

Step 2

Since our denominators match, we can add the numerators.

768 + 96 = 864

This yields the answer

Step 3

The last step is to reduce the fraction if we can.

To find out, we try dividing it by 2...

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

No good. So next you try the next prime number, which is 3...

Are both the numerator and the denominator evenly divisible by 3? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

No good. 3 is larger than 2. So we're done reducing.

And we're done! Here's the final answer to 64/16 + 6/12