What is 15/60 + 10/11?

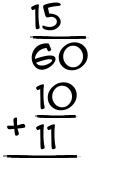
Here's how you add

Step 1

We can't add two fractions with different denominators (the bottom number). So you need to get a common denominator - both bottom numbers need to match. To do this, you'll multiply the denominators times each other... but the numerators have to change, too. They get multiplied by the other term's denominator.

So we multiply 15 by 11, and get 165, then we multiply 60 by 11 and get 660.

Do the same for the second term. We multiply 10 by 60, and get 600, then multiply 60 by 11 and get 660.

So now our fractions look like this:

Step 2

Since our denominators match, we can add the numerators.

165 + 600 = 765

So the answer is:

Step 3

Last of all, we need to simplify the fraction, if possible. Can it be reduced to a simpler fraction?

To find out, we try dividing it by 2...

Nope! So now we try the next greatest prime number, 3...

Are both the numerator and the denominator evenly divisible by 3? Yes! So we reduce it:

Let's try dividing by that again...

Nope! So now we try the next greatest prime number, 5...

Are both the numerator and the denominator evenly divisible by 5? Yes! So we reduce it:

Let's try dividing by that again...

Nope! So now we try the next greatest prime number, 7...

Nope! So now we try the next greatest prime number, 11...

Nope! So now we try the next greatest prime number, 13...

Nope! So now we try the next greatest prime number, 17...

Nope! So now we try the next greatest prime number, 19...

Nope! So now we try the next greatest prime number, 23...

Nope! So now we try the next greatest prime number, 29...

Nope! So now we try the next greatest prime number, 31...

Nope! So now we try the next greatest prime number, 37...

Nope! So now we try the next greatest prime number, 41...

Nope! So now we try the next greatest prime number, 43...

Nope! So now we try the next greatest prime number, 47...

No good. 47 is larger than 44. So we're done reducing.

There you have it! Here's the final answer to 15/60 + 10/11