What is 64/16 + 3/12?

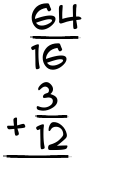
Here's how we add

Step 1

Can you add yet? Nope! The denominators don't match. We need a common denominator. So next we take both denominators and multiply them. Next, take each numerator and multiply it by the denominator of the other term.

So, we multiply 64 by 12, and get 768, then we multiply 16 by 12 and get 192.

Now for the second term. You multiply 3 by 16, and get 48, then multiply 16 by 12 and get 192.

We now have a new problem, that looks like this:

Step 2

Since our denominators match, we can add the numerators.

768 + 48 = 816

That gives us the sum, which is

Step 3

Now, do we need to simplify this fraction?

First, we attempt to divide it by 2...

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

No good. So next you try the next prime number, which is 3...

Are both the numerator and the denominator evenly divisible by 3? Yes! So we reduce it:

So far so good... let's try to divide by that number again.

No good. So next you try the next prime number, which is 5...

No good. 5 is larger than 4. So we're done reducing.

And we're done! Here's the final answer to 64/16 + 3/12