What is 3/20 + 5/9?
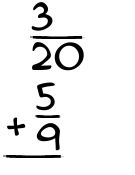
|
This is how you add
|
|||||||||||
Step 1We still have different denominators (bottom numbers), though, so we need to get a common denominator. This will make the bottom numbers match. Multiply the denominators together first. Now, multiply each numerator by the other term's denominator. Now we multiply 3 by 9, and get 27, then we multiply 20 by 9 and get 180. Now for the second term. You multiply 5 by 20, and get 100, then multiply 20 by 9 and get 180. This gives us a new problem that looks like so:
|
|||||||||||
Step 2Since our denominators match, we can add the numerators. 27 + 100 = 127 So what's the answer so far?
|
|||||||||||
Step 3Can this fraction be reduced? First, we attempt to divide it by 2... Nope. Try the next prime number, 3... Nope. Try the next prime number, 5... Nope. Try the next prime number, 7... Nope. Try the next prime number, 11... Nope. Try the next prime number, 13... Nope. Try the next prime number, 17... Nope. Try the next prime number, 19... Nope. Try the next prime number, 23... Nope. Try the next prime number, 29... Nope. Try the next prime number, 31... Nope. Try the next prime number, 37... Nope. Try the next prime number, 41... Nope. Try the next prime number, 43... Nope. Try the next prime number, 47... Nope. Try the next prime number, 53... Nope. Try the next prime number, 59... Nope. Try the next prime number, 61... Nope. Try the next prime number, 67... Nope. Try the next prime number, 71... Nope. Try the next prime number, 73... Nope. Try the next prime number, 79... Nope. Try the next prime number, 83... Nope. Try the next prime number, 89... Nope. Try the next prime number, 97... Nope. Try the next prime number, 101... Nope. Try the next prime number, 103... Nope. Try the next prime number, 107... Nope. Try the next prime number, 109... Nope. Try the next prime number, 113... Nope. Try the next prime number, 127... Nope. Try the next prime number, 131... No good. 131 is larger than 127. So we're done reducing. Congratulations! Here's your final answer to 3/20 + 5/9
|