math help

What is 3/20 + 10/12?

What is 3/20 + 10/12?

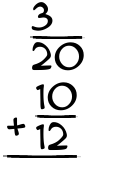
This is how we add

3
20
 +
10
12

Step 1

We still have different denominators (bottom numbers), though, so we need to get a common denominator. This will make the bottom numbers match. Multiply the denominators together first. Now, multiply each numerator by the other term's denominator.

Now we multiply 3 by 12, and get 36, then we multiply 20 by 12 and get 240.

3/20 times 12

Now for the second term. You multiply 10 by 20, and get 200, then multiply 20 by 12 and get 240.

10/12 times 20

This gives us a new problem that looks like so:

36
240
 +
200
240

Step 2

Since our denominators match, we can add the numerators.

36 + 200 = 236

So what's the answer so far?

236
240

Step 3

Can this fraction be reduced?

First, we attempt to divide it by 2...

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

236
240
 ÷ 2 =
118
120

Let's try dividing by that again...

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

118
120
 ÷ 2 =
59
60

Let's try dividing by that again...

Nope! So now we try the next greatest prime number, 3...

Nope! So now we try the next greatest prime number, 5...

Nope! So now we try the next greatest prime number, 7...

Nope! So now we try the next greatest prime number, 11...

Nope! So now we try the next greatest prime number, 13...

Nope! So now we try the next greatest prime number, 17...

Nope! So now we try the next greatest prime number, 19...

Nope! So now we try the next greatest prime number, 23...

Nope! So now we try the next greatest prime number, 29...

Nope! So now we try the next greatest prime number, 31...

Nope! So now we try the next greatest prime number, 37...

Nope! So now we try the next greatest prime number, 41...

Nope! So now we try the next greatest prime number, 43...

Nope! So now we try the next greatest prime number, 47...

Nope! So now we try the next greatest prime number, 53...

Nope! So now we try the next greatest prime number, 59...

Nope! So now we try the next greatest prime number, 61...

No good. 61 is larger than 59. So we're done reducing.

There you have it! Here's the final answer to 3/20 + 10/12

3
20
 +
10
12
 =
59
60
© 2014 Randy Tayler

10/12 + 1/2
10/12 - 1/2
10/12 + 1/3
10/12 - 1/3
10/12 + 2/3
10/12 - 2/3
10/12 + 1/4
10/12 - 1/4
10/12 + 2/4
10/12 - 2/4
10/12 + 3/4
10/12 - 3/4
10/12 + 1/5
10/12 - 1/5
10/12 + 2/5
10/12 - 2/5
10/12 + 3/5
10/12 - 3/5
10/12 + 4/5
10/12 - 4/5
10/12 + 1/6
10/12 - 1/6
10/12 + 2/6
10/12 - 2/6
10/12 + 3/6
10/12 - 3/6
10/12 + 4/6
10/12 - 4/6
10/12 + 5/6
10/12 - 5/6
10/12 + 1/7
10/12 - 1/7
10/12 + 2/7
10/12 - 2/7
10/12 + 3/7
10/12 - 3/7
10/12 + 4/7
10/12 - 4/7
10/12 + 5/7
10/12 - 5/7
10/12 + 6/7
10/12 - 6/7
10/12 + 1/8
10/12 - 1/8
10/12 + 2/8
10/12 - 2/8
10/12 + 3/8
10/12 - 3/8
10/12 + 4/8
10/12 - 4/8
10/12 + 5/8
10/12 - 5/8
10/12 + 6/8
10/12 - 6/8
10/12 + 7/8
10/12 - 7/8
10/12 + 1/9
10/12 - 1/9
10/12 + 2/9
10/12 - 2/9
10/12 + 3/9
10/12 - 3/9
10/12 + 4/9
10/12 - 4/9
10/12 + 5/9
10/12 - 5/9
10/12 + 6/9
10/12 - 6/9
10/12 + 7/9
10/12 - 7/9
10/12 + 8/9
10/12 - 8/9
10/12 + 1/10
10/12 - 1/10
10/12 + 2/10
10/12 - 2/10
10/12 + 3/10
10/12 - 3/10
10/12 + 4/10
10/12 - 4/10
10/12 + 5/10
10/12 - 5/10
10/12 + 6/10
10/12 - 6/10
10/12 + 7/10
10/12 - 7/10
10/12 + 8/10
10/12 - 8/10
10/12 + 9/10
10/12 - 9/10
10/12 + 1/11
10/12 - 1/11
10/12 + 2/11
10/12 - 2/11
10/12 + 3/11
10/12 - 3/11
10/12 + 4/11
10/12 - 4/11
10/12 + 5/11
10/12 - 5/11
10/12 + 6/11
10/12 - 6/11
10/12 + 7/11
10/12 - 7/11
10/12 + 8/11
10/12 - 8/11
10/12 + 9/11
10/12 - 9/11
10/12 + 10/11
10/12 - 10/11
10/12 + 1/12
10/12 - 1/12
10/12 + 2/12
10/12 - 2/12
10/12 + 3/12
10/12 - 3/12
10/12 + 4/12
10/12 - 4/12
10/12 + 5/12
10/12 - 5/12
10/12 + 6/12
10/12 - 6/12
10/12 + 7/12
10/12 - 7/12
10/12 + 8/12
10/12 - 8/12
10/12 + 9/12
10/12 - 9/12
10/12 + 10/12
10/12 - 10/12
10/12 + 11/12
10/12 - 11/12