What is 21/63 + 4/6?

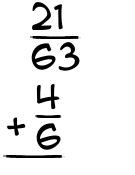
This is how we add

Step 1

Of course, you can't add two fractions if the denominators (bottom numbers) don't match. To get a common denominator, multiply the denominators together. Then we fix the numerators by multiplying each one by their other term's denominator.

Now you multiply 21 by 6, and get 126, then we multiply 63 by 6 and get 378.

Do the same for the second term. We multiply 4 by 63, and get 252, then multiply 63 by 6 and get 378.

The problem now has new fractions to add:

Step 2

Since our denominators match, we can add the numerators.

126 + 252 = 378

The sum we get is

Step 3

The last step is to reduce the fraction if we can.

To find out, we try dividing it by 2...

Are both the numerator and the denominator evenly divisible by 2? Yes! So we reduce it:

Now, try the same number again.

Nope. Try the next prime number, 3...

Are both the numerator and the denominator evenly divisible by 3? Yes! So we reduce it:

Now, try the same number again.

Are both the numerator and the denominator evenly divisible by 3? Yes! So we reduce it:

Now, try the same number again.

Are both the numerator and the denominator evenly divisible by 3? Yes! So we reduce it:

Now, try the same number again.

Nope. Try the next prime number, 5...

Nope. Try the next prime number, 7...

Are both the numerator and the denominator evenly divisible by 7? Yes! So we reduce it:

Now, try the same number again.

No good. 7 is larger than 1. So we're done reducing.

Congratulations! Here's your final answer to 21/63 + 4/6