What is 3/12 + 10/11?
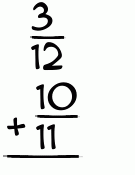
|
Let's add
|
||||||||||||||||||
Step 1We can't add two fractions with different denominators (the bottom number). So you need to get a common denominator - both bottom numbers need to match. To do this, you'll multiply the denominators times each other... but the numerators have to change, too. They get multiplied by the other term's denominator. So we multiply 3 by 11, and get 33, then we multiply 12 by 11 and get 132. Do the same for the second term. We multiply 10 by 12, and get 120, then multiply 12 by 11 and get 132. So now our fractions look like this:
|
||||||||||||||||||
Step 2Since our denominators match, we can add the numerators. 33 + 120 = 153 Now we have an answer.
|
||||||||||||||||||
Step 3Last of all, we need to simplify the fraction, if possible. Can it be reduced to a simpler fraction? To find out, we try dividing it by 2... Nope! So now we try the next greatest prime number, 3... Are both the numerator and the denominator evenly divisible by 3? Yes! So we reduce it:
Let's try dividing by that again... Nope! So now we try the next greatest prime number, 5... Nope! So now we try the next greatest prime number, 7... Nope! So now we try the next greatest prime number, 11... Nope! So now we try the next greatest prime number, 13... Nope! So now we try the next greatest prime number, 17... Nope! So now we try the next greatest prime number, 19... Nope! So now we try the next greatest prime number, 23... Nope! So now we try the next greatest prime number, 29... Nope! So now we try the next greatest prime number, 31... Nope! So now we try the next greatest prime number, 37... Nope! So now we try the next greatest prime number, 41... Nope! So now we try the next greatest prime number, 43... Nope! So now we try the next greatest prime number, 47... No good. 47 is larger than 44. So we're done reducing. There you have it! Here's the final answer to 3/12 + 10/11
|